Hi! I'm building AI that helps us co-invent the future at Asari AI; I'm its Founder and CEO. We're hiring!
Most recently, I led an AI research team that developed the AI Economist, a framework to use deep reinforcement learning and GPU-accelerated multi-agent simulations for economic policy design to improve social welfare.
My research has been covered in US media, e.g., MIT Technology Review, and international media, e.g., the Financial Times (UK), het Financieele Dagblad, de Volkskrant (NL), FastCompany World-Changing Ideas. I was also on Dutch radio to talk about the AI Economist!
Before working on AI, I was a theoretical physicist. You can always wake me up for superstrings and topological branes.
I grew up in the Netherlands (gezellig!), and have lived in the UK and the US.

- Co-organized the AI x Economics workshop at HBS, July 31-August 1, 2023. Report forthcoming!.
- Led the AI Economist team as a Lead Research Scientist at Salesforce Research.
- Researched multi-agent, robust machine learning and more during my PhD at Caltech (Physics, 2018), advised by Yisong Yue.
- Worked on robust deep learning with Yang Song, Thomas Leung, and Ian Goodfellow as a Google intern in 2015.
- Answered natural language questions with deep learning at Google Brain with Andrew Dai and Samy Bengio in 2016.
- Went down the rabbit hole on math and theoretical physics at Utrecht University from 2006-2011.
- Wrote a master's thesis on exotic dualities in topological string theory with Robbert Dijkgraaf & Stefan Vandoren.
- Received the 2011 Lorentz Graduation Prize from the Royal Netherlands Academy of Arts and Sciences [1, 2].
- Visited Harvard University in 2010 & did Part III Mathematics at the University of Cambridge in 2011-2012.
MACHINE LEARNING - RESEARCH HIGHLIGHTS

Mitigating climate change requires international cooperation. But without a central authority, nations need to negotiate and reach agreements, and do so out of their own volition. Which protocols and agreements are self-incentivizing and lead to better climate outocmes? Find out more at AI for Global Climate Cooperation!
AI for Global Climate Cooperation: Modeling Global Climate Negotiations, Agreements,
and Long-Term Cooperation in RICE-N
[Paper] [Website]
A position paper that surveys the potential of next-gen simulations.
Simulation Intelligence: Towards a New Generation of Scientific Methods
[Paper]
On a framework to develop and deploy machine learning systems.
Technology readiness levels for machine learning systems
[Paper]

We released WarpDrive, an open-source framework for deep multi-agent RL on a GPU. It's orders of magnitude faster than CPU + GPU solutions, and scales well across thousands of environments and agents. In 2d Tag, we get ~3 million steps per second with 2000 parallel environments and 1000 agents!
WarpDrive: Extremely Fast End-to-End Deep Multi-Agent Reinforcement Learning on a
GPU
[Paper] [Blog post] [Code]
Using hierarchical curricula, we can find approximate game-theoretic equilbria in real business cycle models that include consumers, firms, and a government. These are stylized macroeconomic models of the real world.
Finding General Equilibria in Many-Agent Economic Simulations using Deep
Reinforcement Learning
[Paper] [Code]
Time and energy are scarce. The AI Economist can also analyze organizations with rationally inattentive agents that pay a cost to observe information, and therefore need to choose what to pay attention to. This is a form of bounded rationality, which models human behavior.
Modeling Bounded Rationality in Multi-Agent Simulations Using Rationally Inattentive
Reinforcement Learning
[Paper (coming soon)] [Code]
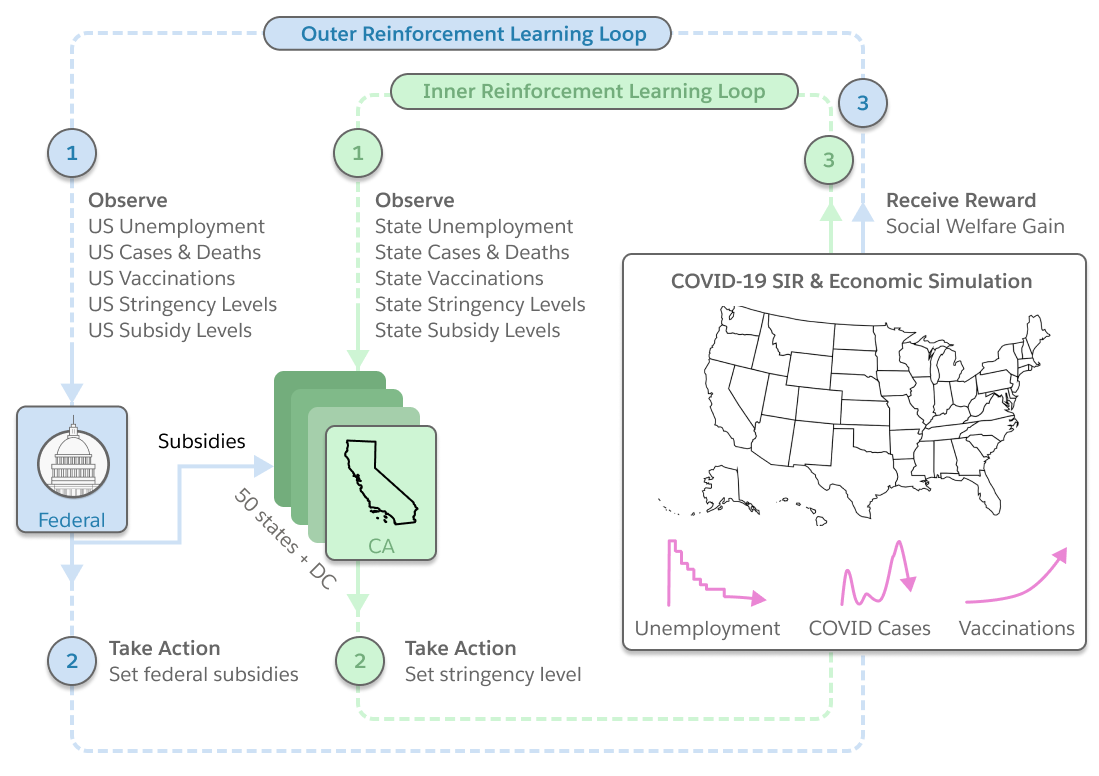
The AI Economist learns public health and economic policies in a data-driven pandemic-economic simulation of COVID-19. AI policies can halve deaths compared to the real world, while maintaining similar unemployment levels. The policies also are interpretable and robust.
Building a Foundation for Data-Driven, Interpretable, and Robust Policy Design using
the AI Economist
[Paper] [Web Version] [Web
Demo] [Blog
post] [Code]
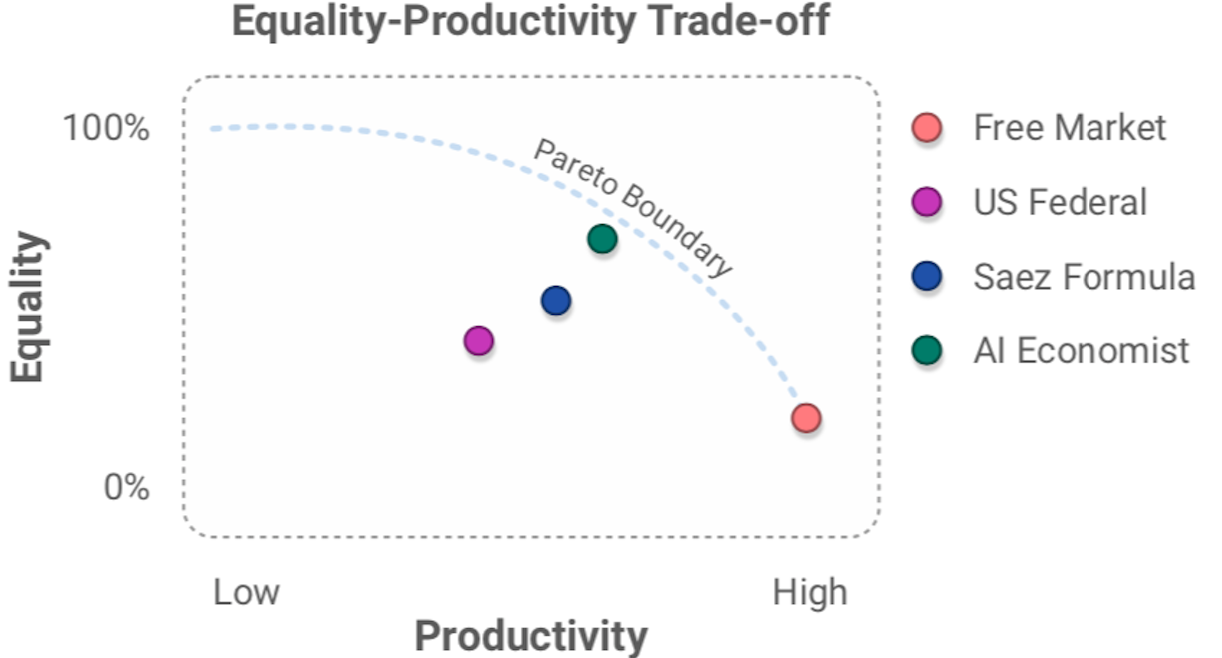
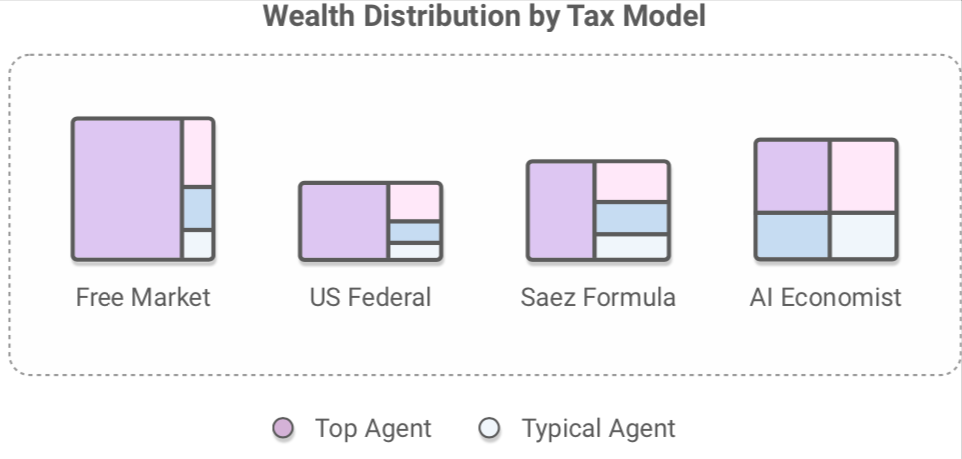
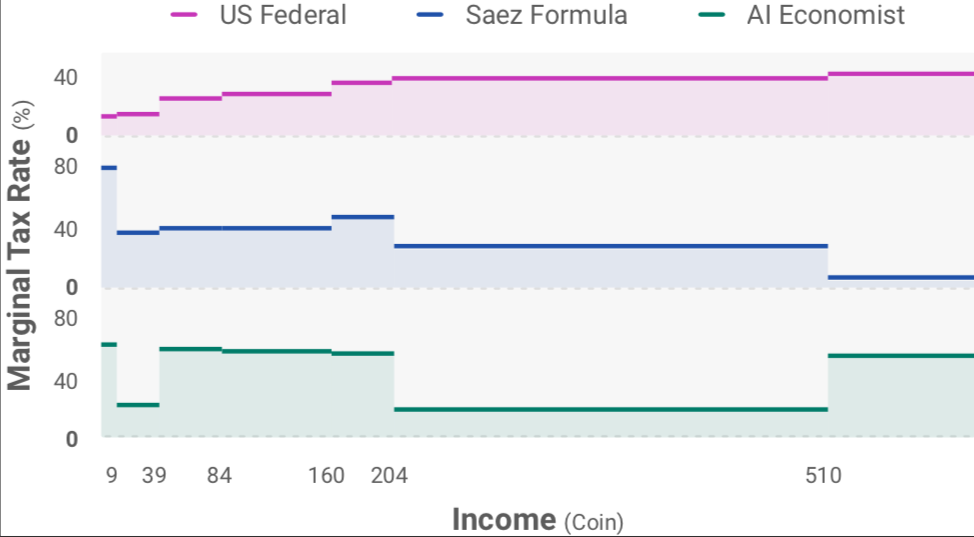
The AI Economist uses reinforcement learning to learn tax policies in AI simulations. AI tax policies yield at least 16% higher equality-times-productivity than prominent tax models. It also shows promising results in human studies, in which real people earn real money in our economic simulation.
The AI Economist: Taxation policy design via two-level deep multiagent reinforcement
learning
[PDF]
The AI Economist: Improving Equality and Productivity with AI-Driven Tax
Policies
[Press Release] [Blog] [PDF]
The AI Economist: Improving Equality and Productivity with AI-Driven Tax
Policies
[Press Release] [Blog] [PDF]
The AI Economist: Optimal Economic Policy Design via Two-level Deep Reinforcement
Learning
AI can talk about physics! We train deep language models to generate descriptions of physics. 👉👉 Next stop: describing string theory!
ESPRIT: Explaining Solutions to Physical Reasoning Tasks
[PDF]
Sibling Rivalry dynamically trades off between exploration and exploitation, and automatically avoids local optima and enables RL policies to converge to the true optimal policy more easily.
Keeping Your Distance: Solving Sparse Reward Tasks Using Self-Balancing Shaped
Rewards
[PDF]
We show that under the reparameterization trick, one can derive generalization bounds for reinforcement learning.
On the Generalization Gap in Reparameterizable Reinforcement Learning
[PDF]
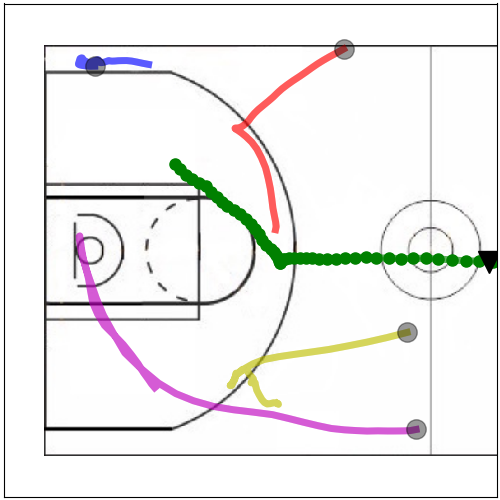
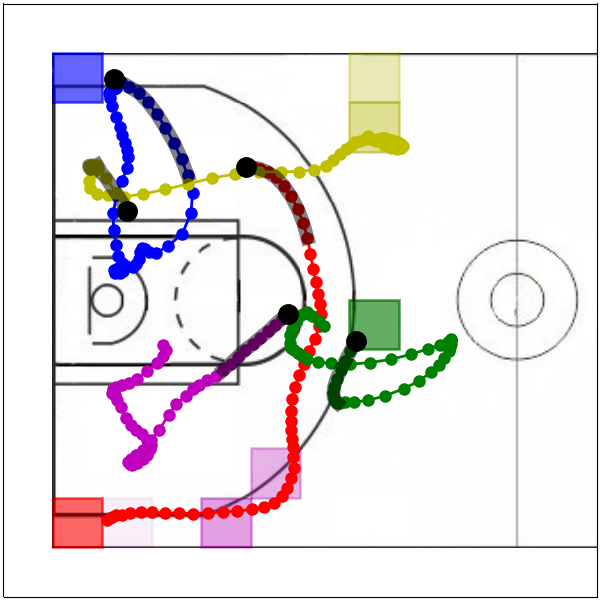
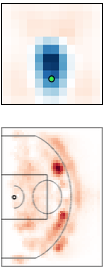
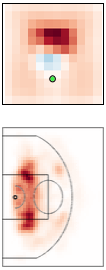
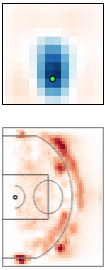
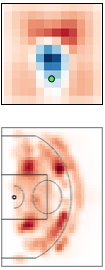
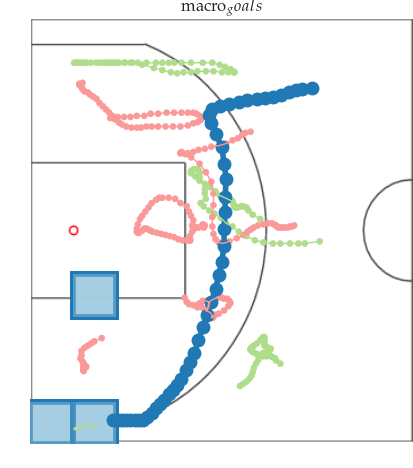
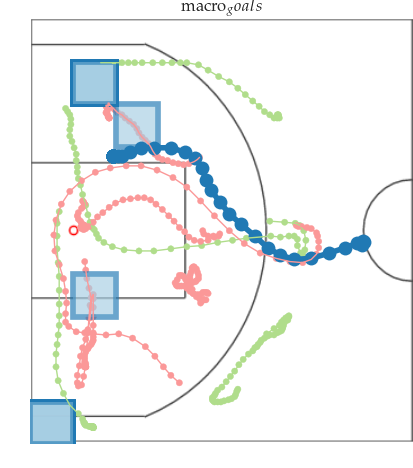
Multi-resolution learning accelerates learning interpretable tensor models from high-resolution spatiotemporal data. Such tensor models can model rich multi-agent correlations, as in basketball and social interactions between fruitflies.
Multiresolution Tensor Learning for Efficient and Interpretable Spatial
Analysis
[PDF]
Multi-resolution Tensor Learning for Large-Scale Spatial Data
[PDF]
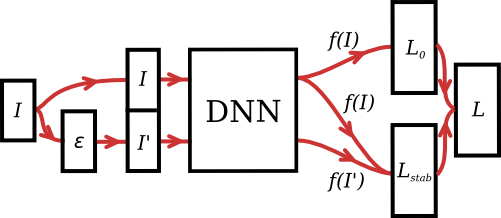
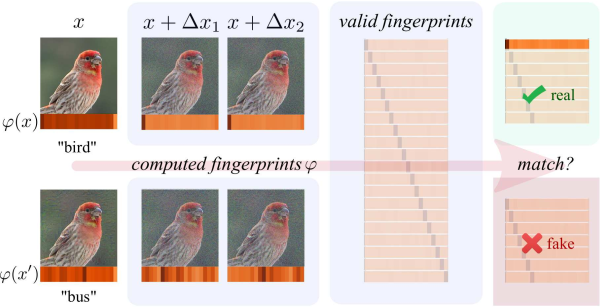
Stochastic data augmentation makes neural networks more robust to input perturbations, such as JPEG corruption. Deployed in Google Image Search!
Improving the Robustness of
Deep Neural Networks via Stability Training
[PDF]
THEORETICAL PHYSICS
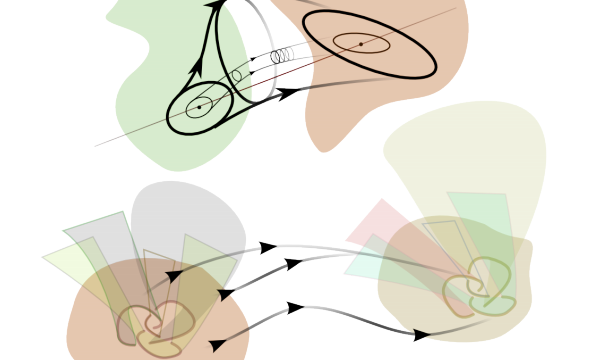
My master's thesis on relating different types of topological branes using exotic dualities. First introduced by Edward Witten, you can construct exotic duals by using Morse theory on complexifications of quantum fields.
Exotic path integrals and dualities,
[PDF]

Janus particles are synthetic particles that could provide localized drug delivery, for example. We study the electromagnetic screening effects of Janus particles in plasmas by (numerically) solving the non-linear Poisson-Boltzmann equation. This paper built on my bachelor's thesis, joint with Elma C. Gallardo.
Screening of Heterogeneous Surfaces: Charge Renormalization of Janus
Particles
[PDF]